Calculus‚ explored through algebraic‚ numerical‚ and graphical methods‚ benefits from resources like textbooks and online platforms – offering a balanced learning experience.
These editions‚ including those from 2020 and earlier‚ integrate technology for enhanced understanding‚ utilizing the “rule of four” for comprehensive problem-solving.
The approach emphasizes interpreting differential equations with slope fields and assessing series convergence‚ alongside approximating functions with Taylor polynomials for accuracy.
The Rule of Four
The Rule of Four represents a cornerstone pedagogical approach in modern calculus education‚ advocating for a comprehensive understanding achieved through four interconnected representations. These are algebraic‚ numerical‚ graphical‚ and verbal interpretations of calculus concepts.
This method‚ prominently featured in texts like “Calculus: Graphical‚ Numerical‚ Algebraic‚” encourages students to analyze problems from multiple perspectives. For instance‚ a function can be defined algebraically with an equation‚ explored numerically through tables of values‚ visualized graphically on a coordinate plane‚ and described verbally in plain language.
The integration of technology enhances this approach‚ allowing for dynamic visualizations and efficient calculations. By mastering all four representations‚ students develop a deeper‚ more robust grasp of calculus‚ fostering problem-solving skills and conceptual clarity. This balanced method is crucial for success in Advanced Placement Calculus and beyond.
Historical Development of Calculus
Calculus didn’t emerge in a vacuum; its development spans centuries‚ building upon the work of mathematicians from diverse cultures. Early foundations were laid by ancient Greek mathematicians exploring areas and volumes‚ foreshadowing integral calculus. Later‚ 17th-century giants‚ Isaac Newton and Gottfried Wilhelm Leibniz‚ independently formulated the core principles of both differential and integral calculus.
Newton‚ focused on physics and motion‚ developed calculus as a tool to describe physical laws. Leibniz‚ with a more systematic algebraic approach‚ created notation still used today. Subsequent mathematicians refined these concepts‚ expanding applications to various fields.
Modern calculus textbooks‚ like “Calculus: Graphical‚ Numerical‚ Algebraic‚” reflect this historical evolution by integrating graphical and numerical methods alongside traditional algebraic techniques‚ offering a multifaceted understanding of this powerful mathematical discipline.

Algebraic Foundations of Calculus
Calculus relies heavily on a strong algebraic base‚ encompassing functions‚ limits‚ and derivatives‚ as presented in texts like “Graphical‚ Numerical‚ Algebraic” editions.
Functions and Their Graphs
Functions form the bedrock of calculus‚ demanding a thorough understanding of their behavior and representation. Texts like “Calculus: Graphical‚ Numerical‚ Algebraic” meticulously explore function definitions‚ domain and range analysis‚ and various function types – polynomial‚ trigonometric‚ exponential‚ and logarithmic – all crucial for subsequent calculus concepts.
Graphical representation is paramount; visualizing functions allows for intuitive comprehension of limits‚ continuity‚ and derivatives. These editions emphasize carefully aligned examples and exercises‚ updated with current data‚ to solidify this understanding. The ability to interpret a function’s graph‚ identify key features like intercepts and asymptotes‚ and sketch graphs accurately is fundamental.
Furthermore‚ understanding function transformations – shifts‚ stretches‚ and reflections – is essential for manipulating and analyzing functions effectively. The interplay between algebraic manipulation and graphical interpretation is consistently reinforced‚ providing a holistic approach to mastering functions and their graphs‚ preparing students for advanced calculus topics.
Limits and Continuity
Limits are foundational to calculus‚ defining how a function behaves as its input approaches a specific value. Texts like “Calculus: Graphical‚ Numerical‚ Algebraic” meticulously explain limit calculations‚ employing algebraic techniques to evaluate indeterminate forms and graphical methods to visualize limit behavior. Understanding one-sided limits and infinite limits is also crucial.
Continuity‚ a direct consequence of limits‚ describes functions without breaks or jumps. These resources demonstrate how to identify points of discontinuity – removable‚ jump‚ and infinite – and their implications. The concept of the Intermediate Value Theorem is often explored‚ showcasing the power of continuity.
The integration of numerical approaches‚ like examining function values close to a point‚ reinforces the understanding of limits and continuity. Updated examples and quick quizzes‚ found in various editions‚ ensure students grasp these core concepts‚ preparing them for the study of derivatives and integrals.
Derivative as a Function

The derivative‚ representing the instantaneous rate of change of a function‚ is central to calculus. Resources like “Advanced Placement Calculus” demonstrate how to define the derivative as a limit‚ utilizing algebraic manipulation to find derivative formulas. Visualizing the derivative as the slope of a tangent line is emphasized through graphical representations.
Understanding the derivative as a function itself is key; texts explore its domain‚ range‚ and properties. Numerical methods‚ such as approximating derivatives using difference quotients‚ provide practical insights. The connection between differentiability and continuity is thoroughly explained‚ highlighting the conditions required for a function to be differentiable.
These editions‚ updated with current examples‚ offer cumulative quick quizzes to reinforce comprehension. The “rule of four” – algebraic‚ numerical‚ graphical‚ and verbal – is consistently applied‚ fostering a holistic understanding of the derivative as a function.

Numerical Methods in Calculus
Calculus utilizes numerical techniques – like Riemann Sums and the Trapezoidal Rule – to approximate solutions when algebraic methods are insufficient‚ aided by graphical analysis.
Approximating Derivatives
Approximating derivatives becomes crucial when analytical solutions are complex or impossible to obtain‚ leveraging numerical methods alongside algebraic foundations and graphical interpretations.
These methods often involve calculating the slope of a secant line as an estimation of the instantaneous rate of change‚ effectively mimicking the derivative’s definition.
Resources like the “Calculus: Graphical‚ Numerical‚ Algebraic” editions emphasize this approach‚ demonstrating how to estimate derivatives using difference quotients and analyzing the resulting approximations.
This involves evaluating function values at closely spaced points and computing the average rate of change between them‚ providing a tangible link between the derivative’s concept and its practical computation.
Furthermore‚ understanding the limitations of these approximations – such as the impact of step size on accuracy – is vital for reliable results‚ enhancing the overall comprehension of calculus principles.
Numerical Integration: Riemann Sums and Trapezoidal Rule
Numerical integration techniques‚ like Riemann Sums and the Trapezoidal Rule‚ provide methods to approximate definite integrals when finding an analytical solution proves challenging‚ bridging algebraic concepts with numerical computation and graphical visualization.
Riemann Sums approximate the area under a curve by dividing it into rectangles and summing their areas‚ while the Trapezoidal Rule utilizes trapezoids for a more refined approximation.
Textbooks such as “Calculus: Graphical‚ Numerical‚ Algebraic” detail these methods‚ showcasing how to apply them and analyze their accuracy.
Understanding the impact of partition size on the approximation’s precision is crucial‚ as smaller partitions generally yield more accurate results.
These techniques offer a practical approach to calculating areas and volumes‚ solidifying the connection between calculus and real-world applications.
Solving Equations Numerically
Solving equations numerically becomes essential when analytical solutions are unattainable‚ employing iterative methods to approximate roots with increasing precision‚ blending algebraic principles with numerical techniques and graphical interpretation.
Methods like Newton’s Method refine initial guesses through tangent line approximations‚ converging towards a root with each iteration.
Resources like “Calculus: Graphical‚ Numerical‚ Algebraic” demonstrate these algorithms‚ emphasizing the importance of initial value selection and convergence criteria.
Understanding potential pitfalls‚ such as divergence or slow convergence‚ is vital for successful implementation.
These numerical approaches extend beyond simple equations‚ finding applications in complex systems modeled by differential equations‚ offering practical solutions in various scientific disciplines.
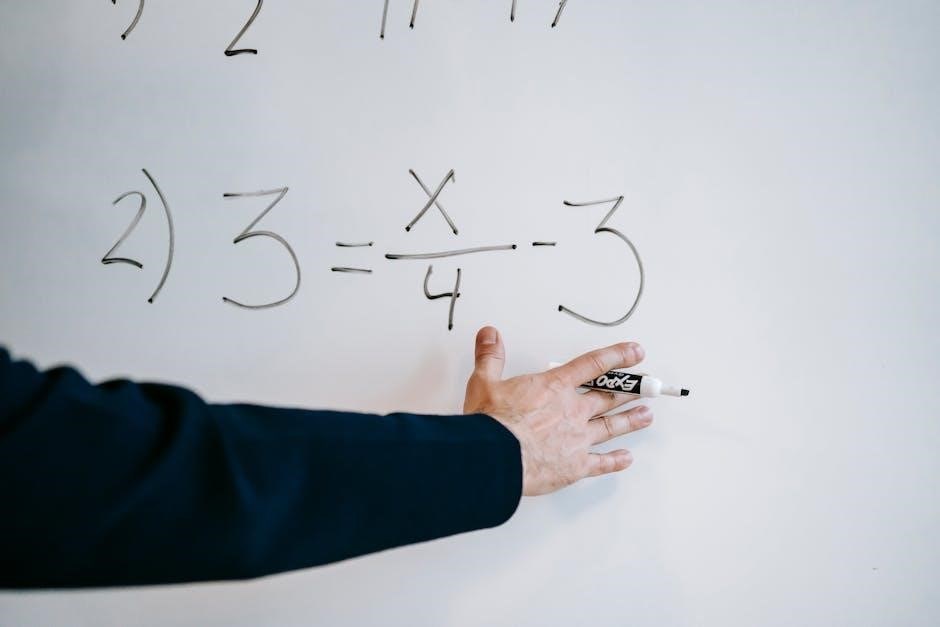
Graphical Interpretation of Calculus
Calculus concepts gain clarity through graphical analysis‚ visualizing limits‚ continuity‚ and derivatives‚ enhancing understanding alongside algebraic and numerical methods‚ as textbooks demonstrate.

Visualizing Limits and Continuity
Understanding limits graphically involves examining function behavior as inputs approach specific values‚ revealing potential discontinuities or approaching a defined value. This visual approach‚ central to calculus‚ complements algebraic evaluations and numerical approximations‚ offering a robust comprehension of function behavior.
Continuity‚ a cornerstone of calculus‚ is readily visualized by observing unbroken function graphs; any breaks‚ jumps‚ or holes indicate discontinuities. Resources like textbooks – including editions from 2020 and earlier – emphasize this graphical interpretation alongside algebraic definitions and numerical tests.
The interplay between these methods – algebraic‚ numerical‚ and graphical – provides a multifaceted understanding of limits and continuity‚ crucial for grasping more advanced calculus concepts. This holistic approach‚ often termed the “rule of four”‚ is consistently integrated into modern calculus learning materials.
Understanding Derivatives Graphically
Derivatives‚ representing instantaneous rates of change‚ are powerfully visualized as the slope of the tangent line to a function’s graph at a given point. This graphical interpretation provides intuitive understanding‚ complementing algebraic calculation and numerical approximation techniques.
Textbooks‚ including those from 2020 and earlier editions‚ consistently emphasize this visual connection‚ illustrating how the steepness of the tangent line directly corresponds to the derivative’s value. Observing how the tangent line changes across the graph reveals information about the function’s increasing or decreasing intervals.
The “rule of four” – algebraic‚ numerical‚ graphical‚ and verbal approaches – reinforces this understanding. Visualizing derivatives aids in grasping concepts like optimization and related rates‚ making calculus more accessible and intuitive.
Applications of Graphs: Optimization Problems
Optimization problems‚ central to calculus applications‚ are effectively tackled using graphical analysis alongside algebraic and numerical methods. Visualizing functions allows identification of maximum and minimum values‚ crucial for real-world scenarios.
Textbooks‚ like the Advanced Placement Calculus editions‚ demonstrate how to find extreme values by examining a function’s graph and identifying critical points – where the derivative is zero or undefined. These points represent potential maxima or minima.
The “rule of four” emphasizes a holistic approach‚ combining graphical interpretation with algebraic techniques to solve optimization problems. This includes finding intervals of increase/decrease and utilizing the first and second derivative tests‚ all reinforced by visual representations.

Key Calculus Concepts & Techniques
Calculus fundamentals involve differentiation rules‚ the chain rule‚ and implicit differentiation‚ alongside applying derivatives to rates of change and optimization problems.
Differentiation Rules
Differentiation‚ a cornerstone of calculus‚ relies on established rules for efficiently finding derivatives of various functions. These rules‚ presented in resources like the Advanced Placement Calculus textbook‚ streamline the process beyond relying solely on the limit definition.
Fundamental rules include the power rule‚ constant multiple rule‚ sum and difference rules‚ and product and quotient rules. Trigonometric function derivatives‚ such as those for sine‚ cosine‚ and tangent‚ are also crucial. Mastering these allows for quick and accurate calculations;
Furthermore‚ understanding these rules is essential for tackling more complex differentiation techniques like the chain rule and implicit differentiation‚ as highlighted in various calculus editions. These rules‚ combined with graphical and numerical interpretations‚ provide a robust understanding of rates of change.
The integration of technology enhances the application of these rules‚ offering verification and visualization.
Chain Rule and Implicit Differentiation
Chain Rule and Implicit Differentiation are advanced techniques vital for differentiating composite and implicitly defined functions‚ respectively. Resources like the Advanced Placement Calculus textbook dedicate significant attention to these concepts‚ building upon foundational differentiation rules.
The Chain Rule addresses functions within functions‚ requiring careful attention to the derivative of the outer function evaluated at the inner function‚ multiplied by the derivative of the inner function. Implicit differentiation handles equations where variables aren’t explicitly isolated‚ utilizing derivatives to find relationships between rates of change.
These techniques‚ often coupled with graphical and numerical analysis‚ provide a deeper understanding of function behavior. Mastering them is crucial for solving complex problems in related rates and optimization. Technology aids in verifying results and visualizing the impact of these differentiation methods.
These concepts are essential for a comprehensive calculus understanding.
Applications of Derivatives: Rates of Change and Optimization
Derivatives unlock powerful applications in analyzing rates of change and solving optimization problems. Calculus textbooks‚ including those from Finney‚ Demana‚ Waits‚ and Kennedy‚ dedicate chapters to these crucial concepts‚ often utilizing real-world examples.
Understanding rates of change allows us to model and predict how quantities evolve over time – velocity‚ acceleration‚ and growth rates are prime examples. Optimization‚ conversely‚ focuses on finding maximum or minimum values of functions‚ essential in engineering‚ economics‚ and various scientific fields.
Graphical and numerical methods complement algebraic techniques‚ providing visual confirmation and approximate solutions. Technology enhances these explorations‚ enabling complex function analysis and efficient solution finding. These applications demonstrate calculus’s practical relevance and problem-solving capabilities.
These concepts are essential for a comprehensive calculus understanding.

Advanced Topics & Resources
Calculus extends to integrals‚ differential equations‚ and Taylor series‚ enhanced by technology and resources like textbooks offering algebraic‚ numerical‚ and graphical approaches.
Integration‚ fundamentally the inverse operation of differentiation‚ expands upon calculus’ core concepts‚ offering a powerful toolkit for solving a diverse range of problems. Resources like the “Calculus: Graphical‚ Numerical‚ Algebraic” editions provide a multifaceted approach to understanding this crucial topic.
These texts often demonstrate integration through various methods – algebraic manipulation‚ numerical approximations like Riemann sums and the trapezoidal rule‚ and insightful graphical interpretations. The exploration of integrals builds upon the foundations laid in earlier chapters‚ connecting areas under curves to accumulated quantities.
Furthermore‚ the integration process is often linked to differential equations‚ where finding integrals becomes essential for determining solutions. The use of technology‚ integrated throughout these resources‚ aids in visualizing integrals and verifying solutions‚ solidifying comprehension and analytical skills.
Understanding integrals is pivotal for advanced calculus applications.
Differential Equations and Slope Fields
Differential equations model dynamic systems‚ describing relationships between functions and their derivatives. Calculus resources‚ such as “Calculus: Graphical‚ Numerical‚ Algebraic‚” emphasize both analytical and numerical solution techniques. A key visualization tool is the slope field‚ graphically representing the rate of change of solutions at various points.
These fields‚ constructed using the differential equation‚ provide qualitative insights into solution behavior without requiring explicit formulas. Algebraic methods‚ when applicable‚ offer precise solutions‚ while numerical approaches – like Euler’s method – approximate solutions when analytical methods fail.
The interplay between graphical and analytical techniques is crucial for understanding the behavior of solutions. Texts integrate technology to generate slope fields and visualize numerical solutions‚ enhancing comprehension. Mastering differential equations is essential for applications in physics‚ engineering‚ and other scientific disciplines.
Taylor Polynomials and Series

Taylor polynomials approximate functions using infinite sums of terms based on their derivatives at a single point. These polynomials‚ and their infinite series counterparts‚ provide powerful tools for function approximation and analysis within calculus. Resources like “Calculus: Graphical‚ Numerical‚ Algebraic” demonstrate how to construct these polynomials and assess their accuracy.
The Lagrange error bound‚ a key concept‚ quantifies the difference between the function and its Taylor polynomial approximation. Graphical representations help visualize the approximation and error; Numerical methods are used to calculate polynomial coefficients and evaluate series convergence.
Understanding Taylor series requires a strong algebraic foundation and an appreciation for the interplay between derivatives and function behavior. These series are fundamental in various applications‚ including solving differential equations and evaluating complex functions.
